■代表的な解析的不等式
これらの不等式は、高校では学ばず、入試問題の中に隠れていて、出会うたびに苦労しながら解いていた部類の問題です。これらをあらかじめ学んでおけば、試験で出会っても先が見えて解きやすく、不安もなく挑戦できる、ぜひ学んでおきたい内容です。それぞれ少し解説が長いので、２つの頁に分けます。

●ベルヌーイの不等式
さまざまな背景を持つ不等式であり、基本的な性質は「n次曲線（n≧2）が（1,1）における接線より上の領域に存在することから生じています。過去に出題された入試問題は若干古いのですが、結果が簡単な不等式なので、さまざまな場面に登場する可能性があります。ｎ次項を1次項で評価できるという、すさまじい効果のある不等式です。

［解説］ベルヌーイの不等式

[B]体積一定で表面積最小の直円柱の問題（2001年東京女子医大）
本問では途中でベルヌーイの不等式を利用します。

[B]ベルヌーイの不等式も利用できる問題（1997年一橋大1）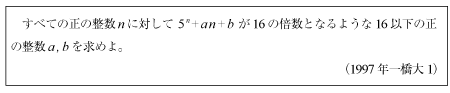

[C]ネピア数の数列の単調増加を示す問題（有名問題）



●ヤングの不等式とヘルダーの不等式
イエンゼンの不等式から導かれる、半端な指数を含む不等式です。半端な指数を含む不等式の証明には対数が必要であり、試験場で出会ったら相当焦る不等式です。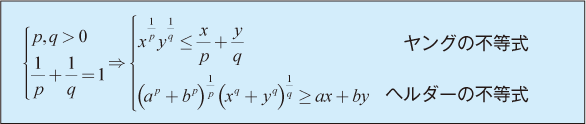

［解説］ヤングの不等式とヘルダーの不等式

●イェンゼンの不等式
わかってみれば内容は簡単な凸曲線の性質にもとづく不等式です。この不等式の発想を利用すると、むずかしい問題が簡単に解けることがあります。また、n次の相加平均≧相乗平均の証明にも利用できます。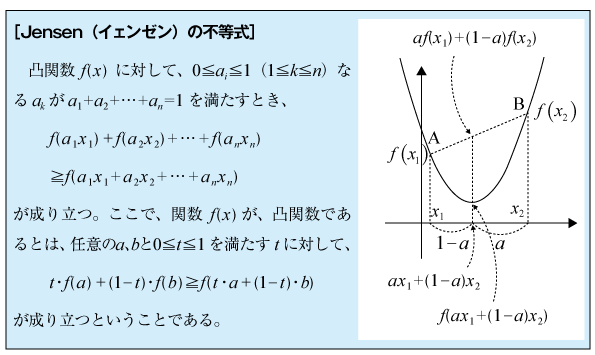

［解説］イェンゼンの不等式
それにしてもあまり名前の知られていない不等式の関連問題がこんなにおおくあることには驚きを禁じ得ません。
 
[C]n=2のイェンゼンの不等式の問題（2007年青山学院大／経済4）
上に凸の関数の重心位置が曲線よりも必ず下にあることが利用できる問題です。「イェンゼンの不等式により」とは書けないので、「三角形の重心」の考え方を利用します。

[B]3次関数/凸関数の不等式の問題（2010年東北大文系1）

[C]イェンゼンの不等式の問題（2014年横浜市大／医2） 

[C]イェンゼンの不等式と対数関数の問題（2014年日本医科大2）
イェンゼンの不等式を平均値の定理などで証明する問題です。

[C]sinαsinβsinγの最大値を求める問題（1999年京大理系後期2）