■場合の数

組合せ記号nCrが登場する問題には「慣れ」が必要です。順列・組合せなどの「場合の数」と「確率」は数Aに属しますが、組合せ記号nCrを利用する二項定理は数Ⅱに属します。確率漸化式は数Bで解説します。

●場合の数と確率（数A）
確率には、「とびとびの事象」（離散事象）を対象とする「離散確率」と、正規分布のように連続的に事象が分布する「連続確率」とがあり、前者は数A、後者は数Bに属します。離散確率は、確率の数学のなかでもやさしい分野の数学であり、ある事象の起きる確率とは、その事象が起きる「場合の数」の「すべての場合の数」に対する比です。
そしてこの場合の数を計算する方法が次の５つの手法です。「場合の数を求めよ」だけの問題は珍しかったのですが、最近増えつつあるので、確率の項と分離させました。本稿では場合の数を解説し、こちらで確率を解説します。

• 順列
• 組合せ
• 重複順列
• 重複組合せ
• 同じものを含む順列

 確率では、次のような事象を考えると計算が簡単になります。その場合、事情を表すのに「論理記号」と「集合記号」のいずれを使っても表すことができますが、確率の計算では集合記号を使う方が簡単です。
　　　　　　　　　　　　　　　　　　　　　論理記号　　集合記号

• 余事象： 　特定の事象が「起こらない」という事象     ¬Ａ                 Ａバー
• 積事象： 　複数の事象が両方起こる事象                     Ａ⋀Ｂ              Ａ∩Ｂ
• 排反事象： 複数の事象が同時に起こらない事象           Ａ⋀Ｂ              Ａ∩Ｂ=∅            
• 和事象： 　複数の事象のいずれかが起こる事象           Ａ⋁Ｂ              Ａ∪Ｂ

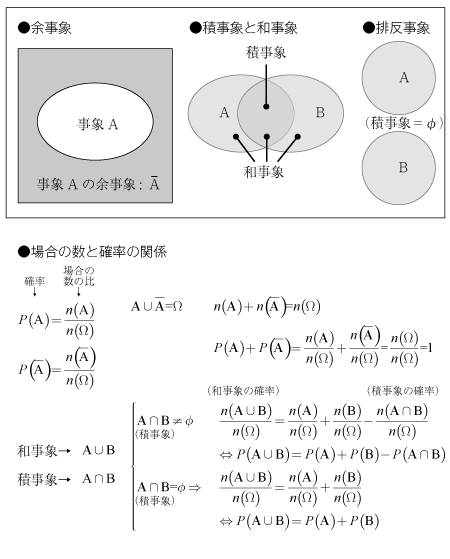
もっとも有用なのが「余事象」という考え方です。たとえば「ある数が5で割り切れる」という事象Aに対し、「ある数が5で割り切れない」という事象Aバー(_A)を「事象Aの余事象」といいます。ある数が「5で割り切れる」ということと「5で割り切れない」ということとは、どちらかが起きて同時には起きない（両立しない）事象であり、このような関係にある事象を「排反事象」とよびます。
排反事象がおきる確率の総和は全事象の確率の和なので１です。たとえばP(A)を求めたい場合に、P(A)よりもP(_A)の方が計算が簡単な場合には、P(A)ではなくP(_A)を計算して1から引けばP(A)が得られます。
事象の確率は、場合の数n(A)と確率P(A)のどちらでも記述でき、問題に応じて計算が簡単な方で計算します。

●組合せ記号
下に組合せ記号（Combination）の意味するところとその性質を示します。組合せ記号ではn-rとrを交換しても値は変わりません。それは、「n個の中からr個を選ぶ」ことと「n個の中から残すr個を選ぶ」こととは同じことを意味するからです。 

なお、組合せ記号の操作にかかわるむずかしい問題は、二項定理・多項定理であつかいます。

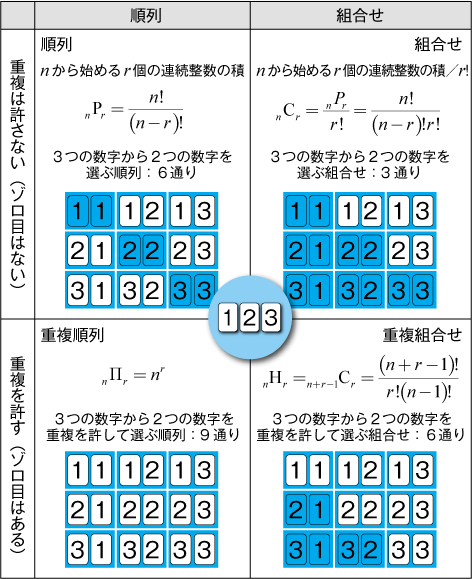
●順列・組合せと重複順列・重複組合せ
順列と組合せ、重複順列と重複組合せの違いの認識は重要であり、これらを区別して認識できれば、後は計算問題となります。順列と組合せの違いは順序を区別するかどうか、重複順列と重複組合せの違いは「同じものが含まれるかどうか」です。具体例を示します。１から３までの３つの数字のカードがあって、そのカードを並べる「場合の数」の考え方は次の通りです。 

• 順列：　　　　　　(1,2), (1,3), (2,3), (2,1), (3,1), (3,2)の６通り
• 組合せ：　　　　　(1,2), (1,3), (2,3)の３通り
• 重複順列：　　　　(1,1), (1,2), (1,3), (2,1), (2,2), (2,3), (3,1), (3,2), (3,3)の９通り
• 重複組合せ：　　　(1,1), (1,2), (1,3), (2,2), (2,3),(3,3)の６通り

●重複組合せの公式と方程式の問題


［例題］組合せの例題

［例題］数字の例題

［例題］順列・組合せの場合の数と確率の例題

[B]７つの数から6桁の数を作る問題（2017年日大／医21）

[B]指定値より小さい３桁の数を作る問題（2017年東海大／医212）

[C]0か1を同数並べる並べ方の数の問題（2015年阪大理系5）

[C]かならず0を含む数字の問題（2011年大阪府立大）


●同じものを含む順列
まぎらわしいのが次の３つの場合の数の考え方です。

• A：重複順列（異なるn個のものから重複を許してr個を取り出して並べた順列の総数）
• B：同じものを含む順列（n個のもののうち、同じものが含まれているときの順列の総数）
• C：重複組合せ（異なるn個のものから重複を許してr個を取り出す組み合わせの総数）

AとCの違いは上の例でわかるでしょうから、AとBの違いを説明します。Aの場合は「異なるn個のもの」のそれぞれの個数には上限がないのですが、Bの場合は「ものによって個数の上限がある」上に「あるものすべてを並べなければならない」ので、重複しない順列から始めて、重複度で割る必要があります。具体例で説明します。

• ［重複順列］a、b、cの３つの記号を重複を許して6個並べる並べ方は3^6=729通り。
• ［同じものを含む順列］aが3個、bが2個、cが1個ある、この6個の並べ方は(3+2+1)!/3!2!1!=60通り。
• ［重複組合せ］a、b、cの３つの記号を重複を許して6個選ぶ組合せの数は3H6=8C6=8C2=28通り。

［例題］
[A]場合の数の問題（2016年慶応／医11）

[B]同じものを含む順列の例題（2010年関西学院大／理工1）
［同じものを含む順列］に関しての典型的な「最短経路問題」です。他の問題はこの問題のバリエーションです。

[B]格子の中に空白がある場合の例題（追加予定）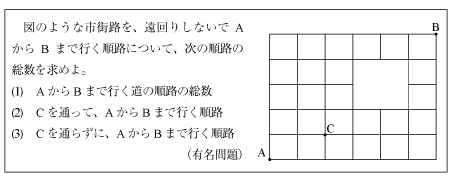


［入試問題］
[B]各桁の数が順に大きくなる4桁の数の問題（2015年日大／医24）

[C]碁盤上に碁石をおく場合の数の問題（2016年慶應大／総合政策1）

[C]立方体の各面を塗る場合の数の問題（2016年順天堂大／医11）
[
[C]一筆書きの数の問題（2008年京大文系5）