■図形と方程式

図形問題を解くには高校数学には大きく分けて5つのテクニックがあり、問題によって使える方法が限られますが、どのテクニックを使うかが勝敗の分かれ目になります。

• 図形と方程式（数Ⅱ）
• 三角関数（数Ⅱ、角度のあつかいに便利）
• ベクトル（数B、角度と内分点のあつかいに便利）
• 複素数平面（数Ⅲ、回転のあつかいに便利）
• 2次曲線（数Ⅲ）

数Ⅲに含まれる2次曲線は、内容としてはそんなに難しいものではないので、文系受験生も理解しておく方が問題の背景がよく理解できます。これらの問題はお互いに共通する部分が多いのですが、余りに問題が多くなったので、あつかいにくくなり、上の5つに分割して収録しました。

●正領域・負領域の問題
　直線や曲線があれば、xy平面はその正領域・負領域に分割されます。「1次関数によって分割された正負領域の問題」や「２次関数によって分割された正負領域の問題」が、2015年愛知教育大や2005年京大で出題されています。
[例題]
[B]直線と正負領域の例題

[入試問題]
[B]直線と正負領域の問題（2015年愛知教育大4）

[C]２次関数と正負領域の問題（2005年京大文1理1）

[C]三角領域と放物線の包含関係の問題（2015年昭和大／医 22）

[D]2変数関数が正値を返すab平面領域の図示の問題（2000年東大文科2）


●点と直線の距離の公式を使う問題
この公式を使う用途は非常に多いのですが、ここでは内接円の問題だけを示しておきます。
[A]点と直線の距離の公式を証明する問題（2013年阪大文系1）

[B]３つの直線の内接円の問題（2014年早稲田大／人間科学3）

[B]３つの直線の内接円の問題（2014年横浜市大／医12）

[C]空間図形と不等式の問題（2010年日本医科大2）


●相加平均≧相乗平均の関係を使う図形問題（数Ⅱ）
[B]単位円上の三角形の面積を最大化する問題（2011年東工大3）

[B]正方形内部の菱形の面積の問題（2006年阪大理系5）

[C]相加平均≧相乗平均を使う図形問題（2012年東大文科2）

[C]相加平均≧相乗平均だけでは解けない図形問題（2008年東大理科4）


●放物線と図形に関する問題（数Ⅱ）
[B]放物線と円の問題（2014年慶応大／理工14）

[B]放物線と3つの共有点を持つ円の半径の問題（2016年東京医科大22）

[B]角の二等分線と放物線との交点の問題（2017年東京医科大11）

[B]放物線と２直線が１点で交わる条件の問題(2006年京大文系1)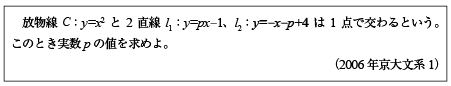

[B]２放物線に接する２直線の方程式を求める問題（2015年東京医科大12）

[B]放物線上の2点を線対称にする直線の傾きの問題（2001年一橋大2）

[C]放物線と円の問題（2012年慶応大／医3）

[C]放物線に接する円の数の判別の問題（2024年東大理4）

[C]放物線の３接線による三角形の垂心の問題（2017年東京理科大／理／応用数学12）

[C]２つの円と共有点を持つ放物線の頂点が存在領域の問題（2009年一橋大3）

[C]図形に関する応用問題（2022年東大理3）


●円の弦に関する問題
[B]円の弦がつくる三角形の面積の最大値の問題(2014年自治医大11)
[B]円の接線が他の円とつくる弦の長さの問題(2014年自治医大13)

[B]円の弦がつくる三角形の面積の問題（2011年東大理科1）
本問では４つの解法を示します。先に答えが見つかれば簡単に解けます。数Ⅱの範囲でも解けます。
［解法1］「点と直線の距離の公式」と数Ⅲ微積分を利用する
［解法2］垂線の長さを計算する
［解法3］中心角に三角関数を利用する
［解法4］２次関数を利用する

[B]弦と弧が囲む領域を切る線分の長さの最大値の問題(2012年東大理科1)

[D]円上の定点とx軸上の定点を通過する平行な直線の問題（2005年一橋大2）


●円の接線に関する問題
[B]2つの円の共通接線を求める（新作問題）
解いてみると結構計算が手ごわい問題です。いくつも解法がありますが、すべての方法に慣れておかないと、大変なことになります。こちらでは「円の接線の公式」も利用できます。
［解法1］「円の接線公式」と「点と直線の距離の公式」を利用する
［解法2］「点と直線の距離の公式」と直線の方程式を利用する
［解法3］直線の方程式と判別式＝0を利用する

[B]円と2つの接線に接する円の問題（2014年日大／医2）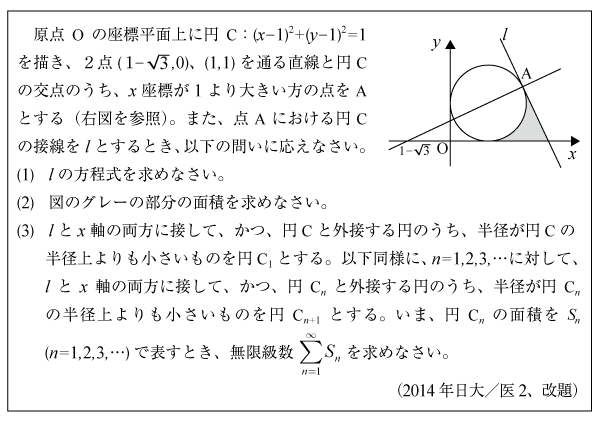

[C]円上でのx/y+x/xの最大値を求める問題（2014年東京医科大12）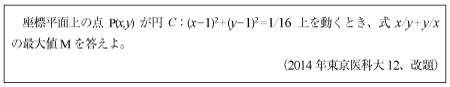

[B]三角形の内外心の問題（2011年日本医科大1）

[C]円の内外接の問題(2009年東大文科1)


●２つの図形の共有点に関する問題
[B]放物線と双曲線の交点を通る円の問題（2019年日本医科大1）


●その他の図形問題
[B]正三角形とその線対称図形の共通部分の面積の問題（2006年一橋大2）

[B]平行四辺形領域の面積の最小値の問題（2017年一橋大4）

[C]三角形の重複部分の六角形の面積の問題（2015年早大／商2）

[B]三角形の３頂点・３辺からの距離の平方和最小化の問題（2016年慶應大／総合政策2）
これら２題は早慶出題合戦でしょうか。

[B]2つの直線のなす角度を最大化する問題（2014年昭和大／医12）
角度をあつかうにはtanかベクトルの内積が必要です。本問ではtanの関数を作ったので、さらに微分が利用できます。

[C]直角三角形の内部点から３辺までの距離の平方和の最小化の問題（2017年早大／商13）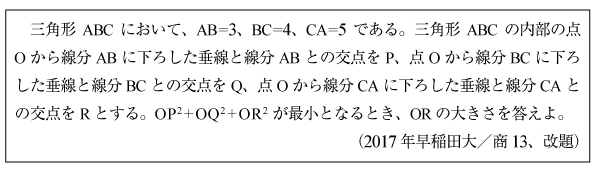

[C]半円上の点の座標を使ってベクトルを構成する問題（2018年千葉大／医8）

角度の扱いにベクトルを利用する、頻出パターンの問題も示しておきます。
[C]ベクトル間の角度の問題（2008年東大文科3）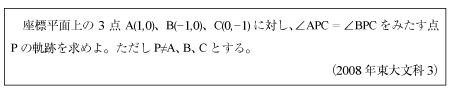

[C]等積変形の問題(2010年東大理科4)

[C]単位円上の回転移動の問題（2014年一橋大3）

[B]計算がかなり大変な直線対称移動の問題（2006年東大理科3）