■大学入試に出題された関数方程式・微分方程式の問題
●関数方程式と微分方程式
関数方程式とは、関数形は与えられずに、関数が満たす方程式だけが与えられてその性質を調べる問題です。ここに微分係数が含まれたものが微分方程式です。関数方程式を解いた結果、微分形が得られてしまう場合もあり、その先に関数形を求めるのは微分方程式の問題になります。
この手の問題では、変数に具体的な値を代入したり、微分演算を行ったりして着手点を探します。多くは指数関数、対数関数あるいは三角関数とそれらの組合せに帰着されます。多項式関数の問題では、次数がキーピントです。これが目算でわかれば大サービス問題です。
したがって、これらの方程式は次の4つにグループ分けできます。
- 多項式関数の関数方程式
- 多項式関数以外の関数方程式
- 微分形に持ち込む関数方程式
- 微分方程式
以下に、考えられるすべてのパターンの問題をそろえました。これだけやっておけば、関数方程式も微分方程式も怖いものなしでしょう。
●多項式関数の関数方程式
[B]関数方程式と有理数の問題(2025年北大文4) 
[B]多項式の関数方程式の問題(2017年東京理科大/理工/情報11)
[B]多項式の関数方程式の問題(2017年昭和大/医245)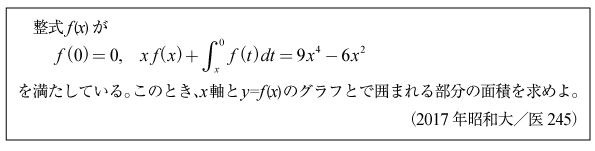
[B]多項式の関数方程式の問題(2009年京大文系2)
[B]多項式関数に関するやさしい関数方程式問題(2018年早大/商13)
[B]簡単な関数方程式の問題(2010年東大文科2)
[B]多項式の関数方程式の変形問題(2011年東大文科1)
[B]2次関数を求める関数方程式の問題(2005年東大文科1)
[B]2次導関数の平方積分を最小化する関数方程式の問題(2002年東大文科3)
[B]やさしい関数方程式の問題(2015年昭和大/医243)
[B]微分方程式の問題(2014年早大/商12)
[C]多項式の関数方程式の問題(2011年日本医科大2)
[C]関数方程式と数列の極限の融合問題(2016年東海大/医23)
[D]整式の積分方程式の問題(2019年早大/商13)
●多項式関数以外の関数方程式
[入試問題]
[B]微分多用の関数方程式の問題(2012年埼玉大文系4)
[B]三角関数を含む関数方程式の問題(2001年東大理科2)
[B]差分方程式から指数関数を導く問題(2000年東大理科3)
[C]2回の微積分が必要な積分方程式の問題(2018年日本医科大3)
[C]双曲線関数を含む関数方程式の問題(2014年阪大理系2)
[C]変数変換が必要な関数方程式と極限値の計算問題(2018年慈恵医大2)
[C]逆関数の関数方程式の問題(2017年慶應大/理工13)
[D]変数変換が必要な関数方程式の難問(2019年東工大2)
●微分形に持ち込む関数方程式
[例題]
[B]関数方程式の基本問題(2003年筑波大理系1)
●変数分離形の微分方程式
微分方程式は、1980年代までは頻繁に出題されていましたが、一時すたれたものの、最近は教科書上で「発展的内容」として取り上げられていることもあり、「変数分離形」に限ってしばしば出題されています。微分方程式は、一種の積分です。下に示すように、左右両辺にそれぞれ関数や変数を分離した場合、「異なる変数」の関数と微分が等号でつながれてているということは、「両辺の差異が、積分して定数になる程度」であるということであり、両辺を積分して積分定数Cを付加し、この積分定数は初期条件で決める、という手順を追います。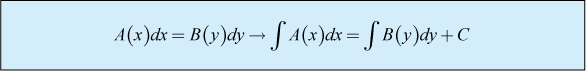

[微分方程式の例題]
極めて簡単な微分方程式問題です。
[B]微分方程式の問題(2011年横浜市大/医14)
[入試問題(計算問題)]
[B]微分方程式の問題(2013年獨協医大5)
[B]微分方程式の問題(2010年同志社大/生命医科3)
[C]関数方程式から変数分離形を積分する問題(2009年慈恵医大3)
[C]対数微分か積の微分を使う微分方程式の問題(2009年横浜市大/医4)
[D]微分方程式の難しい問題(2015年鳥取大/医4)
大学の微分方程式論の中では、常微分方程式の非常に簡単な例なのですが、微分方程式論無しで解くには、かなり大胆な思い付きが必要な問題です。
[D]関数方程式の難しい問題(2017年東京医科歯科大3)
初期値の設定が若干むずかしい問題です。
[入試問題(応用問題)]
[B]円錐形容器内の水に関する微分方程式の問題(2003年北大理系3)
[B]円錐形容器内の水に関する微分方程式の問題(2006年京大理系後期5)
[B]微分方程式と指数・対数の問題(2017年横浜市大/医4)