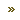■三角不等式

三角不等式は、「三角形のいかなる２辺の長さの和も他辺の長さより大きい」という三角形の構成原則に根差しています。
　　|a|+|b|≧|c|=|a+b|、|b|+|c|≧|a|=|b+c|、|c|+|a|≧|b|=|c+a|
逆に、「三角形のいかなる辺の長さも他2辺の長さの差より大きい」ということから
　　|a|～|b|≦|c|=|a+b|、|b|～|c|≦|a|=|b+c|、|c|～|a|≦|b|=|c+a|
が成立します。
三角不等式は、表現からわかるようにすべての「ベクトル」に対しても成立し、等号成立はベクトルの向きが一致するときです。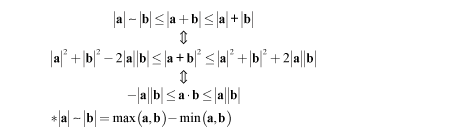

この不等式は、両辺を２乗すると、シュワルツの不等式に帰着されます。三角不等式の等号成立条件は若干複雑で、ベクトルの場合は「向きが同じか反対か」、実数の場合は「符号が同じか逆か」です。
[入試問題]
[B]実数に関する三角不等式の問題（2008年学習院大他）

[B]三角不等式が使えるベクトルの問題（2012年青山学院大／経済32）
この問題は置き換えがキーポイントの、２乗しないで解いて欲しい問題です。

[C]三角不等式が使える無理関数の問題（2009年信州大／医3）
この問題では、無理関数の和の最小値を容易に求めることができます。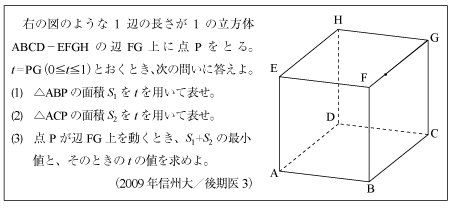

[C]三角不等式と無理数の問題（2017年阪大理系3）

[C]三角不等式の応用問題（2006年一橋大3）

[E]三角不等式などを利用して３次関数の形を決定する問題（2011年阪大理4）