[4] 剰余類・合同式を使う問題

●剰余類を使う問題
整数の証明問題では、数式で計算して証明できるものがあれば「ラッキー」です。剰余類や合同式はそのための手段の最たるものです。「２の剰余類」（奇数または偶数、n=2m+k、k=0,1）、「３の剰余類」（n=3m+k、k=0,1,2）は、かならず試すべきテクニックです。
下に示す2013年阪大の問題のように、問題文が割り算を暗示していない場合にも使えるのがこのテクニックの便利な点です。
●合同式を使う問題
「割れるかどうか」なだ剰余類がよいのですが、「余りはいくらか」という問題においては合同式のほうが便利になります。合同式の場合には、剰余類が加法・減法・乗法において閉じていることを利用します（除法においては閉じていません）。「閉じている」とは、同じ剰余類に属する要素同士の演算の結果が同じ剰余類に属している（外に飛び出さない）ということです。これを合同式の記号で表すと次のようになります。加法・減法の証明はあまりに簡単なので、乗法の場合だけ証明を示しておきます。


[剰余類を使う入試問題]
[A]ユークリッドの補題などの証明問題（2010年神戸大文系3）
「ある素数が 2 つの数の積を割り切れるなら、2 つの数の少なくとも 1 つはその素数で割り切れる。」という命題は「ユークリッドの補題」と呼ばれるものです。

[A]素数性の計算での証明問題（2006年京大理系4）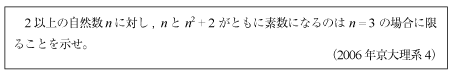

[B]３の剰余類を利用して倍数性を証明する問題（2001年京大文系3）

[B]３の剰余類を利用する証明問題（2004年早大／政経3）

[B]剰余類を使って証明する素数の問題（2019年早大／理工1）

[B]３の剰余類を利用する証明問題（2013年阪大理系3）

[B]３の剰余類と１の３乗根の問題（2018年慶応大／理工12）

[C]３の剰余系を利用して最小値を求める問題（2014年京大理系5）


[合同式を使う入試問題]
[B]合同式を利用する計算問題（2018年順天堂／医12）

[B]３番目に小さい６の倍数の問題（2018年千葉大3）

[C]２桁の整数を10a+bとおく問題（2007年東大文科3）
1の位の数は10で割った余りにほかなりません。

[C]３で割り切れる自然数ｎの３乗・n乗+1を求める問題（2003年一橋大1）

[D]初項が与えられない数列の問題（2019年早大／商3）

[D]整数漸化式の問題（2010年一橋大4）