[5] ガウス記号などの新記号問題

「～を～で表す」という新記号問題の多くは、それを「何か計算できる方法で表す」のがキーポイントであり、これによって計算問題に持ち込めます。そうするとそんなにむずかしくなくなります。「ル・ジャンドルの定理」でもガウス記号が用いられます。
　ガウス記号問題は、方程式・不等式から数列・極限問題まで、すべてを本校に掲載します。

●ガウス記号問題の解き方
「x以下の最大の整数」を[x]と表すのは「ガウス記号」と呼ばれるもので、その簡単な問題は中学・高校入試でも出たことがあるかもしれません。ガウス記号に関しては、
　　　x-1＜[x]≦x　あるいは　[x]≦x＜[x]+1
という関係が成立し、ガウス記号問題はこれらの不等式を使って解きます。方法論がはっきりしているだけ、やさしい問題ともいえます。x-[x]を<x>や{x}と定義したものもガウス記号の亜種です。
[例題]
以下の例題では、[ ]なしの関係でkの上限・下限の見当をつけて、その範囲内でのkを網羅してしまうのも一策でしょう。 次は[ ]の応用問題と[ ]から定義した{ }という記号の例題です。

[入試問題]
ガウス記号問題は、早大／商で高頻度で出題されています。
[B]ガウス記号の1次方程式の問題（2014年早大／商13）

[C]ガウス記号を使った方程式の問題（2015年東海大／医113）

[B]ガウス記号の2次方程式の問題（2011年北大理系1）

[B]ガウス記号を使って約数の数を数える問題（2012年東工大22）

[C]ガウス記号と剰余類の問題（2009年早大／理工1）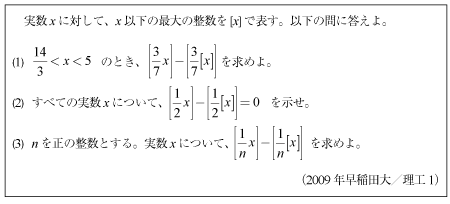

[D]ガウス記号を二重に使った関数の問題（2007年早大／商3）


●ガウス記号を使った数列の問題
[C]ガウス記号を使った数列の問題（2007年上智大／理工2）

[C]小数部分の数列の問題（2011年東大文2理2）

[C]ガウス記号で表された数列の問題（2011年関西学院大理系3）

[C]ガウス記号の逆数の数列の問題（2016年慶應大／環境情報5）

[D]ガウス記号と三乗根の問題（2017年早大／商2）

[D]ガウス記号問題を含む整数に関する難問

[D]ガウス記号を使った方程式と数列の無限和の問題（2010年東工大2）


●ガウス記号極限問題の解き方
[例題]
もう1つの大事な事項はガウス記号と極限計算との関係についての例題です。

[入試問題]
[B]ガウス記号を使った極限値の問題（創価大）

[B]ガウス記号を使った極限の計算問題（2019年早稲田大／理工3）

[C]ガウス記号と区分求積法の問題（2000年阪大理系4）

[C]2n枚のカードからm枚のカードを選ぶ確率の問題（2015年東京医科歯科大1）
ガウス記号を使う確率の問題です。

[C]ガウス記号類似記号を使った極限の収束の問題（2008年東工大2）


●階乗に含まれる素数の数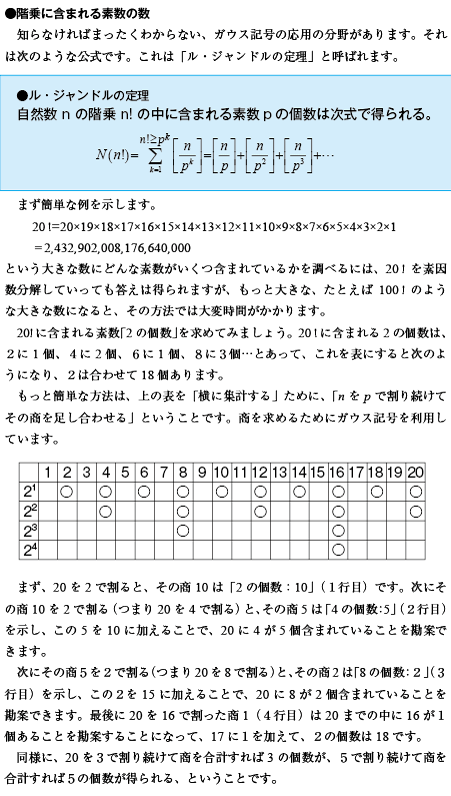


[例題]
[B]階乗の中にある2の数を計算する入試問題（2008早大／教育11）

[B]末尾の０の数を数える問題

[入試問題]
[B]30の階乗30!についての問題（2001年千葉大8）

[B]倍数の数を数える問題（2009年京大文系5）

[C]割り算にかかわる新記号問題（2017年昭和大／医231）

[D]整数にかかわる新記号問題（2008年東大理科5）