■完全対策可能な問題：漸化式の解法

■漸化式の分類
漸化式には、明らかな等差数列・等比数列と特殊な連立漸化式・数学的帰納法などのパターンを除くと、主要なパターンは下記の10種にまとめられます。

漸化式のパターン別分類による解説は当サイトが元祖です！
サイトの拡大・移転完了後、再度大改造します。
他の分野のパターン分類も進化させます。
パターン分類は、小手先の技ですが、手っ取り早い方法ではあります。

本項ではまず、パターンを取得するために、できるだけやさしい問題から紹介します。
漸化式は国立大では単独ではなく確率などの融合問題として出題される場合が多く、その場合には「漸化式を作る」ところから始まります。したがってこの分野はかならず「得意分野」にしておかなければなりません。パターンは随時改善していきます。

これらのパターンは、次の方法のいずれかの組合せで解くことができます。このことを知っておけば慌てないですむでしょう。

• 等差数列や等比数列のパターンに帰着する
• 等差数列の一種である階差数列に帰着する
• 逆数の数列を求める
• 数列を置き換えて解く
• 2項間・3項間・分数数列の特性方程式を解く

上の10パターンの中には、出題頻度が低く若干難しいものもありますが、一度は全パターン解いておくべきです。試験場で初対面、という悲劇は避けましょう。それぞれのパターンを図解します。さらにその後に、４つの番外パターンを紹介します。
これらは10のパターンの簡単な応用であり、別の頁で解説します。
[11]数学的帰納法で解く漸化式
[12]部分和と一般項の混在型
[13]連立漸化式の問題
[14]確率漸化式の問題

●等差数列や等比数列の解説

[例題]


[1]階差数列

[例題]

[入試問題]
[A]階差数列の問題（2003年札幌学院大）
これ以上ないほどやさしい問題です。


[2]２項間特性方程式型

[例題]

[入試問題]
[A]２項間特性方程式型漸化式の問題（2011年慶応大／看護医療23）

[B]２項間特性方程式型漸化式の部分和の評価の問題（2014年自治医科大15）


[3]多項式型
整数nを含む漸化式を、本項では「多項式型」と称します。多くは2項間漸化式ですが、2016年には三項間の多項式型漸化式の難問が横浜市大で出題されました。本頁最下段で紹介します。

[例題]

[入試問題]
[B]多項式型漸化式の問題（2008年関西大／商1）

[B]多項式型の問題（2014年大阪府大／環境4）

[C]多項式型漸化式の問題（2015年東海大／医12）


[4]指数型

[例題]

[入試問題]
[B]指数型漸化式の問題（2007年信州大／工11）

[B]漸化式のやさしい問題（2024年北大文系2）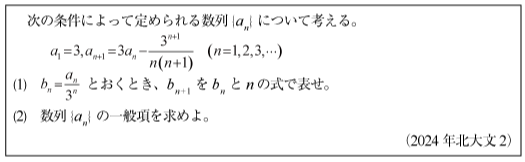

[C]特性方程式・指数型漸化式を解くゲーム確率の問題（2016年千葉大／医7）

[C]数列係数の放物線の図形問題（2007年一橋大2）
指数型と特性方程式型の融合問題で、定数を消去し、階差数列を解く問題です。未定係数法を使っても解けます。


[5]対数型

隣接項間の関係が２乗以上とか分数乗の場合は対数型ということです。
[例題]

[入試問題]
[B]対数型漸化式の問題（2011年静岡大理系1）

[B]対数型漸化式の問題（2017年阪大文系3）

[B]掛け算の漸化式が定める数列の無限和の問題（2016年日大／医24）



[6]公比型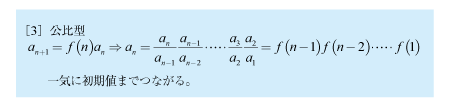

[例題]

[入試問題]
[A]公比型の問題（2007年北里大／医11）


[7]割り算型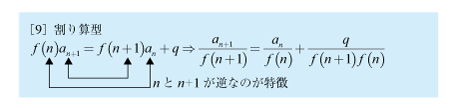

[例題]
[B]多項式割り算型新作問題1

[C]多項式割り算型新作問題2

[入試問題]
[B]公比型漸化式の複合問題（2010年同志社大理系3）


[8]逆数型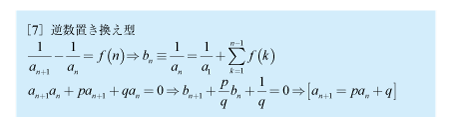

[例題]

[入試問題]
[A]逆数置き換え型の問題（2014年日大／医15）

[B]逆数置き換え型の問題（2013年福岡教育大6）

[B]逆数置き換え型の問題（2004年福岡教育大2）

[C]逆数型かつ多項式型の漸化式の問題（2013年東京医科大11）


[9]分数型
分数型漸化式は逆数型漸化式の一般化された形であり、特に面倒ですが、一般的には誘導が用意されます。初めて見たときや誘導がないときのためには、あらかじめ慣れておくべきでしょう。分数型漸化式の一般的な解法はこちらに紹介しておきます。

[例題]

[入試問題]
● 分子に定数項がない場合
[B]分数漸化式の問題（2010年大阪府大／工11）

[B]分数漸化式の応用問題（2017年日本医科大1）

● 分数数列の特性方程式が解ける場合
[C]分数漸化式の問題（2008年東北大後期4）

[C]分数漸化式と極限値の問題（2015年東工大1）


[10]３項間特性方程式型

2項間漸化式型の漸化式は1次の特性方程式を解くことから始めますが、３項間漸化式型の一般的な解法は２次方程式である特性方程式を解いて2つの特性解を求めてから解きます。この考え方は３項間漸化式の解法で解説しました。この３項間漸化式型の中でも有名なものがフィボナッチ数列が得られる漸化式です。
確率漸化式問題には、２項間・３項間の漸化式を自分で作って解く問題が多く、これらは単独または連立の確率漸化式を立てて解きます。このパターンは難関校で頻出します。
[入試問題]
[B]3項間漸化式の問題（2017年順天堂大／医11）

[B]隣接三項間漸化式のやさしい問題（2012年慶大／医11）

[B]部分和の3項間漸化式の問題（2017年日大／医24）

[B]3項間分数漸化式の問題（2017年昭和大／医131）
「3項間分数漸化式」に一般的な解法はありません。
ではどうやって解くか、ということです。

[C]第２項が欠けた隣接３項間漸化式の問題（2018年愛知医大推薦4）

[D]三項間多項式型漸化式の難問（2016年横浜市大／医13）

[D]係数が確率で変わる3項間漸化式の問題（2011年阪大理5）