■媒介変数曲線問題の基礎

媒介変数表示、極座標と極方程式の関係をまとめておきます。極座標は媒介変数表示の一種であり、xy座標を動径rと偏角θで表したものが極座標、動径rと偏角θがこの場合の媒介変数です。極方程式は、曲線を動径rと偏角θで表したものであり、極方程式は媒介変数表示とは無縁です。これら３つによる円の表示を比較して理解してください。

• xy座標　　　x2+y2=a2
• 極座標　　　x=acosθ、y=asinθ
• 極方程式 　 r=a

まず最初に、極座標で表した基本の媒介変数表示曲線3種の基本例題を挙げます。これらだけで、媒介変数表示曲線に関する入試問題の7割をカバーします。極方程式の場合でもπｘ＾2を計算するのは同じであり、もっとも代表的な「リマソン曲線」を後で紹介します。
[入試問題]
[B]媒介変数曲線のやさしい問題（2012年慶大／医13）

[B]正葉曲線の描画の問題（2018年東京医科大5）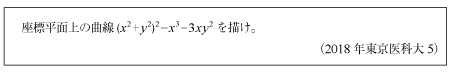

[B]円の伸開線に関する媒介変数表示の問題（2018年順天堂／医13）