■微分不等式問題
本項であつかう「微分不等式問題」とは、「微分を使って不等式を証明する問題」を意味します。微分の基本問題として、出題頻度が非常に大きい問題群です。多くの問題が「差分の振る舞い」を分析して示しますが、その背景には「マクローリン展開」がある問題もあり、先に「マクローリン展開」を学んでおくべきと思います。
[B]微分不等式の問題(2006年筑波大理系2)
[B]微分不等式を用いてネピアの数の近似値を求める問題(2010年横浜市大/医4)
[B]微分不等式の問題(2004年神戸大理系3)
[B]微分不等式の問題(2008年大阪府大/工中期1)
[B]三角関数の微分不等式の問題(2019年筑波大推薦/医1)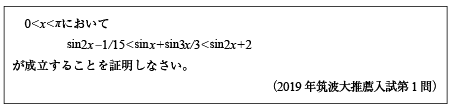
[B]積分結果に関する不等式の伝説の問題(1999年東大理6)
[C]微分不等式の問題(2014年東工大2)
[C]微分も利用する不等式の証明問題(2007年阪大理系2)
[C]不等式の証明問題(2016年東大理科1)
対数微分が必要な問題です。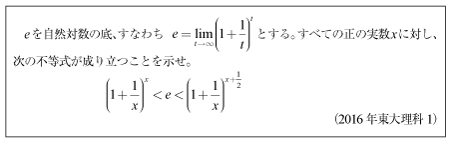
[C]イェンゼンの不等式と対数関数の問題(2014年日本医科大2)
イェンゼンの不等式を平均値の定理などで証明する問題です。
[C]微分不等式の問題(2016年日本医科大2)
[C]微分不等式と関数の値域の問題(2018年阪大理系1) 
[D]微分不等式の問題(2009年東大理科5)
複雑な不等式は、左辺-右辺の式を微分して増減を調べるパターンになります。これも頻出問題です。おおむね力技で解かなければなりません。
 ■近似式
■近似式